Galactic Cartography For Beginners

Gaia project & coordinate systems used

Gaia is an exciting space program that not only is compiling the largest and most accurate star catalog to date, but providing enough data that, for the first time, astrometric studies can be done on what could credibly be termed a galactic scale. Before Gaia, the largest and best source for star positions, parallax measurements, and measurements of proper motion or radial velocity were the catalogs compiled by the Hipparcos program, which had (in their latest and best version) data for about 2.5 million stars. That's a lot of data, but knowing that there are over 5 million stars within 200 parsecs (~650 light years) of our Sun, and hundreds of billions in the Milky Way, this was still only just touching the surface.

The latest Gaia data release contains data on over 1,900,000,000 sources -- I'll use the word "source" instead of "star", because many Gaia sources are multiple star systems that cannot be resolved, and some are non-stellar objects like white dwarfs, brown dwarfs, distant AGNs, planetary nebulae, etc. This catalog may include as many as 1% of all the stars in our galaxy and be almost complete (to at least apparent magnitude 20) within hundreds of parsecs: certainly an unprecedented dataset. Not only is Gaia's EDR3 catalog almost 800 times the size of the Hipparcos Tycho-2 database, but for many sources, the Gaia team was able to make measurements of parallax and proper motion at least an order of magnitude more accurate than Hipparcos'. It's some impressive stuff. You have to work a little to make use of it (it's well over a terabyte download) but if you are even dimly curious about our galaxy it's an absolutely amazing thing.

(I'm going to explain the coordinate system used, as well as some features of the Gaia data. If you don't care about those details, you can jump down the page to the first experiment.)

The first thing we'll want to do is to position as many Gaia sources as possible in 3-D space, so we have an accurate idea of the shape of the nearby galaxy. Gaia provides us with each source's coordinates in the sky (right ascension and declination, essentially longitude and latitude but projected on the celestial sphere.) With Gaia's parallax measurements, we also can make an estimate of the distance to the source in space. (If you're unfamiliar with measuring distance by parallax, Wikipedia's page explains the process and its history at length.)

We could directly convert right ascension, declination, and distance (spherical coordinates) into Cartesian coordinates (x, y, z) using the formulas from your high school trig textbook. If you do so, you'd get a heliocentric coordinate system, where the X-axis is in the direction tangent to the Sun's orbit. The Z-axis would be in the direction of the celestial north pole. The Y-axis would then be fixed as the axis orthogonal to both; if you use the right-hand rule to define the positive direction, then the Y-axis would roughly point away from the center of the galaxy.

You could perform all these experiments using this coordinate system, but it is not frequently used in astrometrics, for a variety of reasons. The Sun has approximately a 62° tilt to the galaxy's plane, for one thing, so any straightforward projections of the galaxy's disk would also be tilted about that amount. While the Y-axis (in the negative direction) does roughly point toward the galaxy's center, it only points in the general direction, several degrees from exact. In studies of stellar kinematics, the direction of galactic rotation may be a more natural choice for an axis than the Sun's particular motion. And, perhaps most importantly of all, most available databases and datasets prefer a different galactic coordinate system, so if you want to compare your results with others', or you want to join other databases to yours, you'll have to convert the coordinate system anyway.

Happily, we can just rotate our axes to the common galactic coordinate system: here, the positive X-axis points at the Milky Way's center, the positive Y-axis is along the direction of galactic rotation, and the positive Z-axis extends through the north galactic pole. (If you're interested in the math, Wikipedia again gives a basic explanation, or see Binney & Merrifield's Galactic Astronomy for in-depth discussion.) After this transformation, we have the 3-D position of stars in the standard galactic coordinate system.

The Gaia EDR3 data release contains parallax measurements for approximately 1.5 billion sources. For every parallax measurement (PX), there is also an error measurement (PX_err), that represents a confidence interval for the true parallax. If a star measures PX of 2 millisecond of arc, with a PX_err of 0.4, then the true parallax is likely in [1.6, 2.4], representing a distance between 416 and 625 parsecs. Note that it is quite possible for the actual error to exceed PX_err; PX_err is just Gaia's best estimate for an error that produces a 1-σ (68%) confidence interval.

The ratio of these two values, PX/PX_err, can be taken as a signal-to-noise ratio representing the reliability of an individul parallax measurement: the higher the ratio, the better. Our example of 2 msec and 0.4 error gives a PX/PX_err = 5. This is about the minimum ratio we should demand; you can see from this example that PX/PX_err = 5 can correspond to an error of about 20% in either direction, or even more than that a third of the time. Out of all the parallax measurements in Gaia EDR3, about 200 million sources, or about 1 in 7 of all sources with parallax measurements, have PX/PX_err ≥ 5.

With more advanced statistical models, and some assumptions about stellar density and distribution in the Milky Way (hopefully assumptions based on good data), it is possible to reduce the average PX/PX_err of distant sources. This sort of correction generally improves the average quality of large samples of data; such adjustments might make any single datapoint more or less accurate, but approaches like this can salvage useful information from the 6 in 7 parallax measurements with high reported errors.

In general, the parallax error increases with distance; almost all sources with low PX/PX_err are very far away, and the farther away you get, the smaller the average PX/PX_err becomes. For the experiments that follow, we will restrict ourselves to Gaia sources with PX/PX_err ≥ 10. This means we'll have many close to exact measurements within 100 parsecs, mostly accurate parallax measaurements at 1,000 parsecs, and increasing noise in the data beyond that.

[Experiment 1] Can you see the shape of the Milky Way's spiral arms in the Gaia data?

At least in our galactic neighborhood, yes! Tracing the entirety, or even most, of the spiral arms is not possible with Gaia data, as few distant sources have sufficiently accurate parallax measurements. However, even a relatively simple approach can reveal information about the shape of the nearby galaxy.

Perhaps the quickest and easiest way to reveal galactic structure on a hundreds-to-few-thousands parsec range (and beyond, with sufficiently clean data) is to plot the positions of the most luminous stars known in the galaxy. Knowing where these stars occur will tell us how we can map the galaxy.

How so? Well, consider the classes of stars involved. Any list of superluminous stars will include O/B supergiants, red supergiants, all hypergiants, and Wolf-Rayet stars. With a few rare exceptions, like cataclysmically variable stars in eruption or classical novae, all superluminous stars share one thing in common: they don't live very long, by the standards of stars, anyway. 20 million years, maybe, at most, with some of these stars having lifespans of 2-3 My or less, almost nothing in astronomical time. They burn hot and die young.

Their relatively short lifespans mean they are almost always found close to where they originally accreted, and are often still inside dense, active star-forming regions (exceptions occasionally occur with "runaway" stars -- these travel at great velocity, thought to be due to a past interaction with an extremely massive body.) And, in spiral galaxies like ours, large star forming regions (and their extremely bright OB associations, and the so-called super star clusters that might contain WR or hypergiant stars) usually show up in and along the spiral arms, where the interstellar medium can become sufficiently dense to form new star clusters.

Some of these stars, by the way, are over one million times as luminous as the Sun. All are at least thousands of times brighter. These are the kinds of stars you can spot in distant galaxies even with relatively modest equipment -- the Gaia EDR3 data includes tens of thousands of superluminous stars and star clusters from the Andromeda and the Triangulum galaxies, over two million light years away, and a few from even further galaxies in the Local Group. It includes many from the Milky Way's satellite galaxies as well.

How do we determine which stars are most luminous? For now, let's do a very simple thing: we have the apparent magnitude of the star from Earth orbit, and a distance approximation that's reasonably accurate (because our signal-to-noise ratio is high.) We know that brightness follows a square law: if a source of fixed luminosity doubles its distance from you, its brightness diminishes by a factor of four. Using that fact, we can calculate what the source's apparent magnitude would be, if it were 10 parsecs away. The apparent magnitude at 10 parsecs is the definition of absolute magnitude, which is directly related to luminosity: the lower the absolute magnitude, the more luminous the source must be.

We select all Gaia sources that satisfy the parallax requirement and that have an absolute magnitude < −3. (Any of the superluminous stars should easily qualify if their distance is in the ballpark, even if there's a little extinction; this range is however high within the top percentile of stellar brightness.) We calculate the position in rectangular coordinates (X, Y, Z) as explained above. Then we make two projections: first we project all of the sources onto the X-Y plane (a view looking onto the galaxy disk), and then we project onto the X-Z plane (a side view of the disk.) These are the results:

---

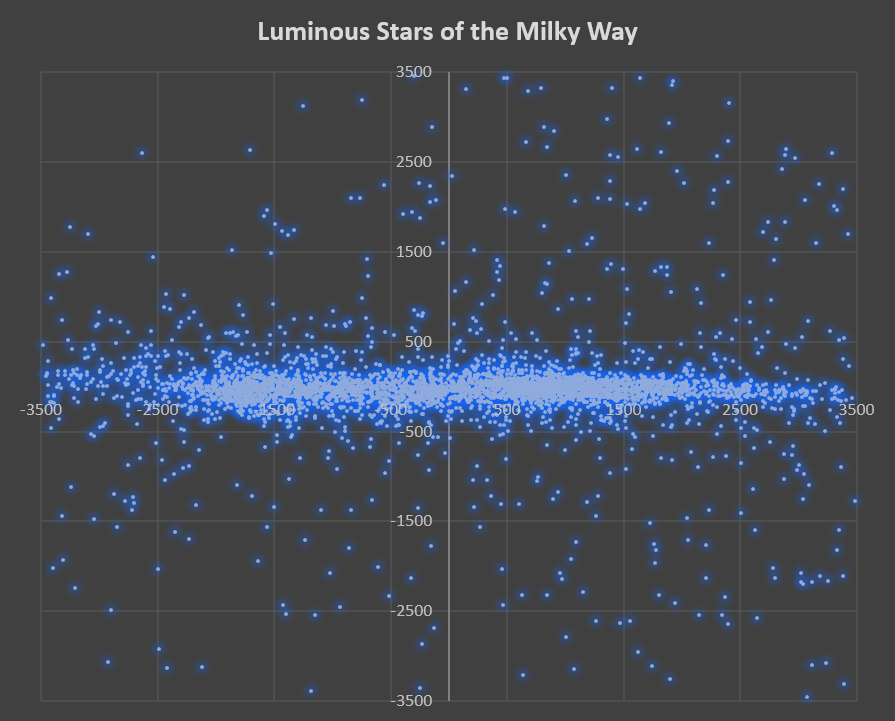
These plots include stars with absolute magnitude < −3 and PX/PX_err > 10. The scale shows parsecs from the Sun (1 pc ≅ 3.26 ly)

This projection onto the X-Y plane is a view looking down from the north galactic pole toward the galactic plane. Here, luminous stars reveal nearby star-forming regions, and indicate the position and rough shape of nearby spiral arms. The Sun is at center. The Orion Molecular Cloud Complex is slightly to the west and northwest of center. The steep diagonal line of stars travelling from SW to NE through the center is the Orion spur (a.k.a. Orion-Cygnus arm) that contains the Sun and the OMCC, whose entire length (~3200 pc) is traced in this plot. The large cloud to the southeast is part of the Scutum-Centaurus Arm (this part containing the massive Carina OB associations), which bends away from there towards the NE, and to the southwest and northwest are parts of the Perseus Arm (Perseus OB1 is found in the cloud in the NW, and the Orion spur meets the Perseus Arm in the SW). In a cloud to the north, near the end of the Orion spur at about (720, 2130), is Cygnus X-1, the first discovered and widely accepted black hole. The 7000 pc × 7000 pc region represents about 4% of the Milky Way's disk, roughly one-fifth its width and one-fifth its length.

In this projection onto the X-Z plane (a "side view" of about one-fifth of the Milky Way's disk), most of the luminous stars trace the galactic plane. Many of the luminous stars in the galactic halo, far above or below the galactic plane, are "runaways", some travelling thousands of kilometers a second. These stars, as they die, create the fast-moving molecular clouds that have been observed littering intergalactic space. Others of these halo stars are members of globular clusters.

---

This simple approach, while it does allow us to plot the length of our local spiral arm and catch a glimpse of the neighboring arms, unfortunately does not penetrate far enough toward the center of the galaxy to spot its central bar(s), due to three factors:

• Interstellar extinction. To look toward the center of the galaxy is to look through thousands of parsecs of gas and dust. The density of this interstellar medium is only a little above vacuum, but the volumes involved are so immense that it's like looking through thick fog; any star will appear much dimmer than it actually is, causing us to underestimate its luminosity.
• Crowding. Stellar densities in the nucleus of the galaxy are, frankly, nuts. Point a telescope almost anywhere in the central bulge, and you'll be greeted with enormous blankets of stars. Any time you have a bright star close to another bright star, it makes either star harder to resolve and measure as an accurate point source. Now imagine, instead of two or three, there are dozens or hundreds or thousands of stars crowded close together, in any direction toward the central bar(s) you look. Only some stars here can be successfully measured within practical error bars.
• Inaccurate parallax measurements. The center of the galaxy is a bit far to get sufficiently accurate parallax from Gaia, even without the crowding issue, and without an accurate distance measurement, how can we accurately estimate the star's luminosity?

Crowding we can't do anything about, but it maybe doesn't matter; as long as we isolate enough superluminous stars to trace the shape, it should be OK. The inaccurate parallax measurements should be partly correctable, and without even requiring sophisticated models; all we have to do is establish a probability that a source is part of the central region of the galaxy, and then we have an approximate distance range ready. If a source is bright enough to be superluminous even at the high distance to the central region, it's 100% good, if not we'll have to take it in a probabalistic fashion. Assign smaller parallaxes a range of higher distances within the central region, and you're good to go.

The interstellar extinction is the biggest problem. This really can make a superluminous object appear merely luminous at our distance, so in order to probe this far in this direction in space, we must make some kind of correction for extinction. (FWIW, interstellar extinction is also an important limiting factor when looking in any other direction in the galactic plane, if you're looking far enough into the distance.)

We can make a reasonably accurate correction for extinction: 3-D measurements of the Milky Way's interstellar medium have been compiled by researchers, and with these "dust maps", we can get a value for extinction in many directions at (almost) any distance. Examples of this data available include Leike, Glatzle & Ensslin's galactic extinction map, which extends 400 parsecs in all directions, and the IPHAS extinction map, which gives cumulative extinction in various bands over half the galactic plane extending out to 6 kpc. There are many others, this page lists more. And if you aren't interested in the dust maps for the sake of having the data, there are resources such as Coryn Bailer-Jones' enormous database of Gaia parallaxes, already corrected for extinction and refined with a photogeometric model taking star color into account.

We'll try this experiment again with corrections for extinction, but for now let's take a look at the local galaxy:

[Experiment 2] The One Million Cubic Parsecs We Call Home